ERATOSTENES Y EL RELOJ DE SOL DE FALTRIQUERA

Llevo unos días probando un reloj de sol de faltriquera, es decir, de bolsillo. Estos relojes se conocen desde tiempos del Egipto ptolemaico, y eran usados por los romanos. Durante el día, claro está, porque cuando llegaba la noche usaban clepsidras, es decir, relojes de agua que transportaban la misma de un recipiente a otro, marcando así cada hora. Se usaban mucho para marcar los tiempos de los oradores.

La base principal de un reloj de sol es que para conocer la hora se necesita saber las coordenadas geográficas para orientar el Plincton, una especie de aguja o triángulo que marca la altura del sol y que permite conocer las coordenadas terrestres.

Al mismo tiempo se necesitaría una brújula, ya que los relojes de arena se deben orientar al norte. La brújula es un invento chino del siglo IX. Antes de la brújula se determinaba el norte con la orientación de los cuerpos celestes, a través del astrolabio, por ejemplo. Por la noche se puede llevar a cabo mediante la orientación de la Estrella Polar, en la Osa Menor. Y en la Gnomónica romana, ya explicada por Plinio el Viejo, es posible conocer el norte, ya que cualquier objeto vertical cayendo en plomada da una sombra, a lo largo del eje norte-sur, cuando llega el mediodía. El mediodía se sabe de inmediato porque es cuando el Sol se eleva más sobre el horizonte, aportando sombras cortas.

Me sorprendió ello, porque si es así significa que desde muy antiguo debió existir algún sistema de coordenadas terrestres, y eso hubiera implicado el conocimiento de una Tierra redonda.

La primera sorpresa es que Dicearco (355-285 a.C.) ya usaba un sistema de coordenadas terrestres para sus mapamundis. Se le conoce como el padre de la geodesia.

Recordemos ahora lo que dijo San Agustín, en el 400 d.C., sobre su idea de una tierra plana que, gracias a la Iglesia Católica, se extendería prácticamente hasta la Edad Media:

«Pero sobre la fábula de que existen los Antípodas, es decir, hombres que viven en el lado opuesto de la tierra, donde el sol se levanta cuando para nosotros se pone, hombres que caminan con sus pies opuestos a los nuestros, eso no es creíble en modo alguno. Y, ciertamente, no se afirma que se haya aprendido tal cosa por conocimiento histórico, sino por conjetura científica, basándose en que la tierra está suspendida dentro de la concavidad del cielo, y que tiene tanto espacio en un lado como en el otro. Por ello afirman que la parte bajo nosotros también debe de estar habitada. Pero no remarcan que, aunque se supone científicamente demostrado que el mundo tiene una forma esférica y redonda, de eso no se sigue que la otra cara de la tierra esté libre de agua; ni tampoco, aunque estuviera realmente libre de agua, se sigue que esté necesariamente habitada».

Y ahora viene la gran sorpresa (tengamos en cuenta que las coordenadas geográficas se adoptaron en 1884 en Washington).

Eratóstenes (276-194 a.C.) fue, como muchos hombres sabios griegos de su tiempo, un célebre matemático, astrónomo, historiador, geógrafo, filósofo y poeta. Estudió en Alejandría y durante algún tiempo en Atenas. Alrededor del año 255 a.C., la gran variedad de sus conocimientos y capacidades para el estudio lo llevaron a ser responsable de la dirección de la Biblioteca de Alejandría, el mayor acervo del conocimiento que existía en su época.

Una de sus principales contribuciones, en la que aplicó sus conocimientos de matemática y astronomía, fue la medición de la circunferencia terrestre a fines del siglo III a.C. Para realizar esta medición el autor se basó en un informe de observaciones en Syena (actual Asuán) que había llegado hasta él, que decía que en ese lugar durante el día del solsticio de verano (21 de junio) al mediodía el Sol no proyectaba sombra alguna; y en el conocimiento que él tenía acerca de que, ese mismo día y a esa hora en Alejandría los edificios sí proyectaban sombra.

Eratóstenes asumió que ambos lugares estaban situados en el mismo meridiano, y a partir de todo esto se abocó a determinar la diferencia de latitud entre los dos lugares. Utilizando un gnomon o un sciotheron (un tipo de reloj de sol) que colocó en Alejandría para medir la longitud de la sombra, y suponiendo que Syena (Asuán) coincidía con el trópico de Cáncer, estableció que la diferencia de latitud entre ambos lugares era igual a 7 ° 12’. Una vez establecida esta diferencia, necesitaba además conocer la distancia entre las dos ciudades. Así, utilizando la distancia conocida entre ellas –igual a 5.000 estadios– y el resultado que había alcanzado sobre la diferencia de latitud, calculó la circunferencia terrestre en 250.000 estadios, resultado al que le agregó, por circunstancias que se ignoran, 2.000 estadios más.

Con esta experiencia de medición Eratóstenes calculó con gran exactitud la circunferencia de la Tierra en 252.000 estadios egipcios (39.690 kilómetros), y logró alcanzar así un resultado muy cercano al valor actual igual a 40.120 kilómetros. Es decir, se equivocó sólo por un escaso margen del 1 por ciento.

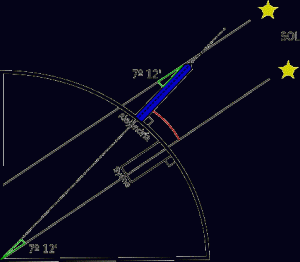Eratóstenes usó para medir los ángulos con las verticales del obelisco de Syena (Asuán) la ley de arcos de círculos relativos a ángulos iguales, que son semejantes. Estando en la Biblioteca de Alejandría, encontró un informe de observaciones sobre Siena, en el que se decía que el día del solsticio de verano (21 de junio) a mediodía, los objetos (como por ejemplo, los obeliscos) no producían sombra y en el fondo de los pozos podía verse la luz del sol. Esto se debe a que está ciudad está sobre la línea del trópico (en realidad, 33′ al norte del Trópico de Cáncer). Eratóstenes realizó observó que, en Alejandría, el mismo día y a la misma hora no se producía este mismo hecho. Asumió de manera correcta que el Sol se encontraba a gran distancia y que sus rayos, al alcanzar la tierra, lo hacían en forma (prácticamente) paralela. Esto ratificaba su idea de que la superficie de la Tierra era curva pues, de haber sido plana, no se hubiese producido esta diferencia entre las dos ciudades.

No cabe duda, desde tiempos de Roma, se conocía la circunferencia de la Tierra.

La última sorpresa es que Posidonio (135 a.C.-51 a.C.) rehízo los cálculos de Eratóstenes, tomando como posición de referencia Canopus, y haciendo una medición más exacta entre Rodas y Alejandría, que estimó de 3.750 estadios griegos. Confundió los estados griegos con los egipcios, y ello le llevó a erra en el cálculo final.

El valor de Posidonio sería el usado por los mapas de Claudio Ptolomeo. Una de estos mapas, el de Ptolomeo, estuvo en manos de Colón, que imaginó que la circunferencia de la Tierra era menor. De ahí su insistencia ante sus hombres para darles a entender que les faltaba poco para llegar a tierra firme.

El gran Eratóstenes padeció una ceguera al final de su vida, lo que le condujo a dejarse morir de hambre, por voluntad propia, el 194 a.C. en su ciudad, Alejandría.